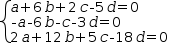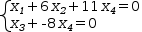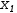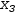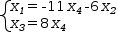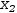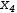←Convert to integralConversions→

3.6.6 Convert to Linear

Linear conversion performs one of two transformations depending on the subject.

  1. If the subject is a tuple of real expressions, a linear-system pseudo-type (§9.5.2), a parametric vector or a linear surface (§9.5.3), it is transformed into an augmented matrix of coefficients.
  2. If the subject is a matrix of scalars, it is transformed into a linear system.

The first kind of linear transformation supports the activity of finding a solution to a system of linear equations. While in matrix form, the coefficients can be transformed to reduced row-echelon form. Then the second kind of linear transformation converts that solution back into a simplified system of equations. The solution can also be expressed in parametric form. See §3.6.7

Prior to considering the subject, if a selection set (see §3.3.7) has been created, a tuple of expressions is introduced to the work space and becomes the active expression, and hence the subject.

A more automated way to solve a system of linear equations is given by Solve , described in §3.7.2.

3.6.6.1 Convert to Matrix

When converting to a matrix, each of the tuple items contributes a row. Nominally, the items are linear equations with a sum of product terms on the left and a constant on the right. The result is an augmented matrix of coefficients with one row for each item, one column for each variable contributed by a product term and a final column for the constant terms. The columns are ordered by sorting the variables they represent. The column with constant coefficients is always the rightmost column. An example is shown in Figure 3.8.

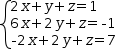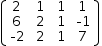(2⋅x+y+z=1, 6⋅x+2⋅y+z=-1, -2⋅x+2⋅y+z=7)ℓ[(2, 1, 1, 1), (6, 2, 1, -1), (, -2, 2, 1, 7)]
(a) Linear System(b) Augmented matrix
Figure 3.8 Convert from linear system to matrix of coefficients

Variations on the source expressions are permitted.

  • If an item is not an equation, it is promoted to an equation whose right side is zero.
  • Product terms can appear on either side of the equation. Coefficients taken from the right side are negated in the resulting matrix.
  • Constants appearing on the left side are subtracted from the column of constant coefficients.
  • The variables in each product term can appear more than once in the same item. The coefficients for similar product-term variables are summed, with signs of each sum term determined by the side of the equation in which the product-term appears.
  • Product terms can contain more than two operands. The coefficient is taken from the leftmost operand if it is constant.
  • Protected subexpressions are treated as coefficients.
  • Any summand that cannot be interpreted as a constant or the product of a constant coefficient with a variable is considered to represent a variable with a coefficient of one.

These variations provide a considerable flexibility in interpreting the source. Figure 3.9 shows source that produces the same matrix as Figure 3.8 (b).

(-1=-2⋅x-y-z, 6⋅x+2⋅y=-z-1, -2⋅x+2⋅y+z-7)ℓ

 


Figure 3.9 Linear system variation

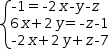
3.6.6.2 Multiple solutions

The linear system

(a+6⋅b+2⋅c-5⋅d=0, -a-6⋅b-c-3⋅d=0, 2⋅a+12⋅b+5⋅c-18⋅d=0)ℓ

 


has the solution

(x_1+6⋅x_2+11⋅x_4=0, x_3+-8⋅x_4=0)ℓ.

 


Isolating x_1 and x_3, the system is

(x_1=-11⋅x_4-6⋅x_2, x_3=8⋅x_4)ℓ.

 


Here, x_2 and x_4 can take on any value, providing a set of solutions. The solution set can be described parametrically using the conversion in §3.6.7.